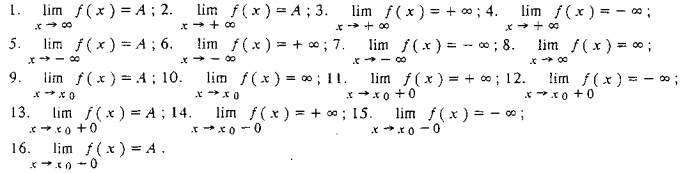Вопросы по математическому анализу (I часть).
1. Метод математической индукции.
1.
Доказательство неравенства Бернулли.
2.
Доказательство формулы бинома Ньютона.
3.
Доказательство формулы
![]()
2.
Аксиомы действительных чисел.
1.
Ограниченные и неограниченные множества.
2.
Определение точной верхней грани множества.
3.
Определение точной нижней грани множества.
4.
Свойства точных граней.
5.
Теорема о существовании точной верхней
(нижней) грани у ограниченного сверху (снизу) множества.
6.
Теорема о единственности точной верхней
(нижней) грани.
7.
Принцип
Архимеда.
8.
Теоремы
о вложенных отрезках.
9.
Определения предела последовательности на
языке є — б .
10.
Теорема о единственности предела
последовательности.
11.
Теорема об ограниченности
последовательности, имеющей предел.
12.
Теорема о сохранении знака сходящейся
последовательности.
13.
Теорема о переходе к пределу в неравенстве.
14.
Теорема о двух милиционерах.
15.
Свойства сходящихся последовательностей.
Свойства б/м и б/б последовательностей.
16.
Бесконечно малые и бесконечно большие
последовательности.
17.
Теорема Вейерштрасса о существовании
предела монотонной ограниченной последовательности.
18.
Число е как предел
последовательности
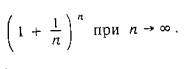
19.
Теорема Штольца.
20.
Теорема Больцано-Вейерштрасса.
21.
Теоремы о подпоследовательностях.
22.
Фундаментальная последовательность.
Необходимые и достаточные условия существования предела последовательности.
(Критерий Коши).
23.
Определение предела функции на языке є —б .
24.
Определение предела функции через предел
последовательности.
25.
Доказательство эквивалентности двух
определений предела функции.
26.
Предел функции в бесконечности.
27.
Арифметические действия с пределами
функции.
28.
Бесконечно малые и бесконечно большие
функции.
29.
Связь бесконечно малых и бесконечно больших
функций.
30.
Определение одностороннего предела функции.